For this module, I learnt about analysing n degree of freedom systems, using D’Alembert, Lagrange or Hamilton’s principle. This also involved learning about holonomic and non-holonomic constraints, expanding my ability to analyse dynamic systems with bars, pendulums and rails as well as mass-spring-damper systems.
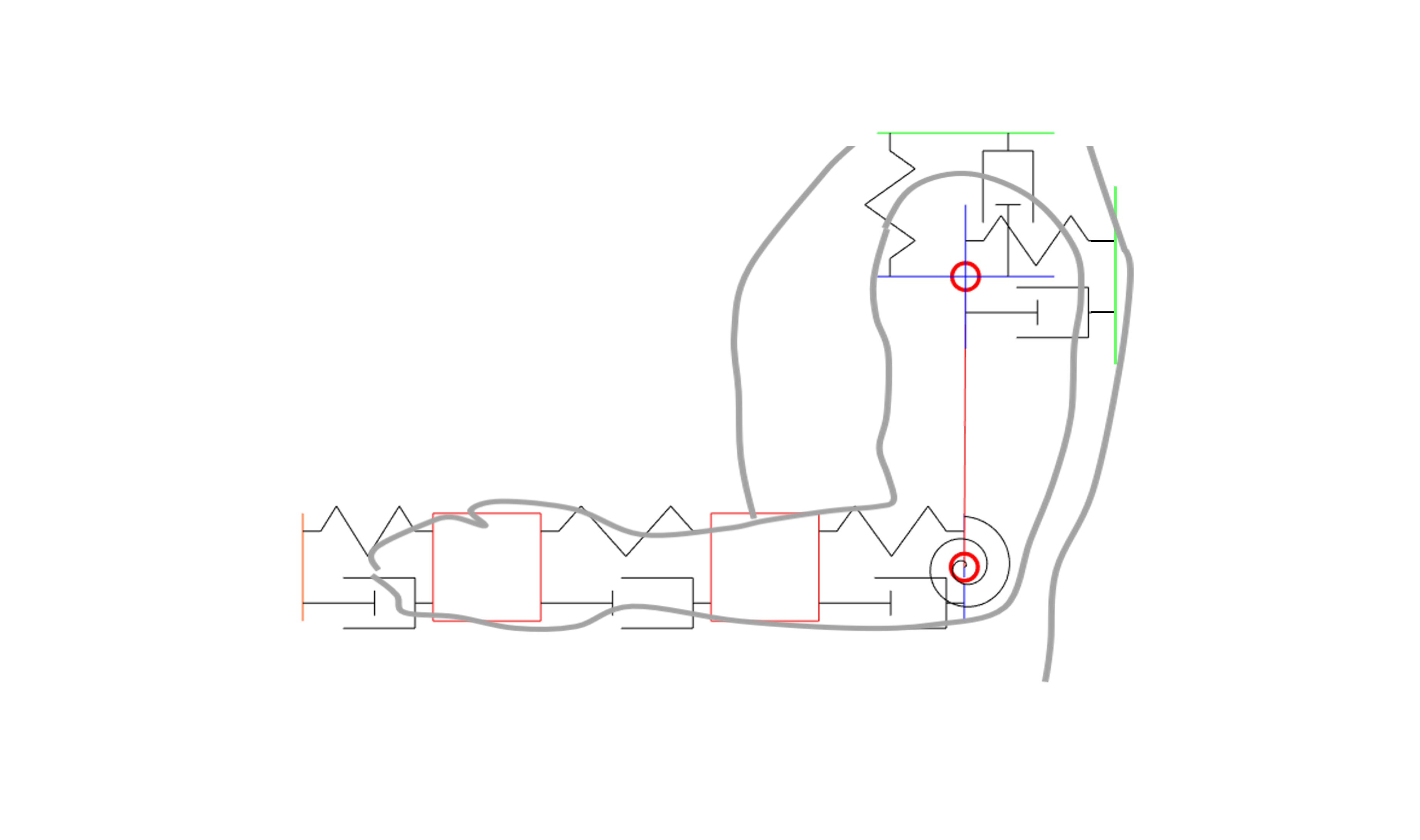
In a group of 4, we conducted a modal analysis of the human arm to understand the resonant frequencies to avoid when designing a new power drill. This involved using Lagrange’s principle to find the equations of motion and then linearising to estimate the eigenfrequencies (i.e. the frequencies the drill should not operate at). My role in the team was to solve the system of differential equations numerically and compare the frequency-domain response against the predicted results from the linearised, analytical equations (see below).
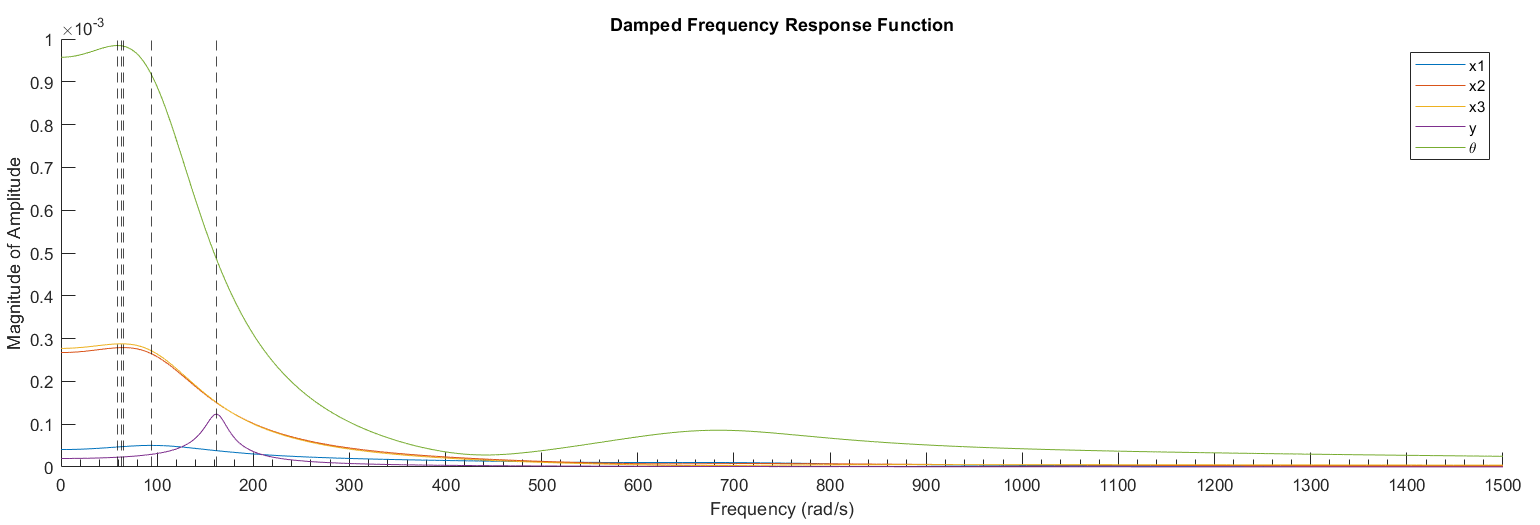
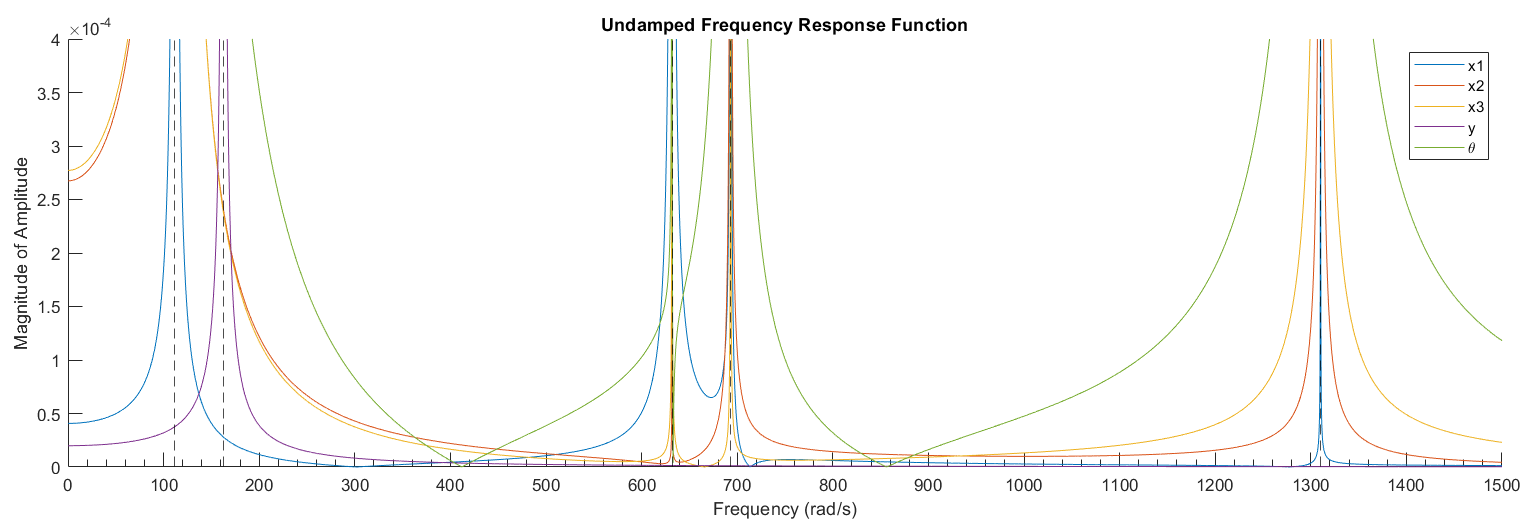
For instance, there is a resonant peak at 100.6Hz (632 rad/s) causing large oscillations in the 1st mass (Figure 6 & 8) representing the mass of a user’s hand, which obviously would not be good. However, in a more realistic scenario with damping (Figure 5 & 7), the magnitude of the oscillations significantly decreases. We concluded the worst frequency was 17.8 Hz (112 rad/s), which could cause major damage to the shoulder (Figure 1 & 2) even with damping. Our predicted resonant frequencies 112, 163, 632, 693 and 1310 rad/s (Figure 8) matched the numerically determined peaks.